Merhaba sevgili arkadaslar,
Oncelikle Fourier Transformu kendi dilimden degil, bir kaynaktan cevirerek aktaracagim size. Fourier Transformu hem guzel hem de faydali bir donusum metodudur. Biz muhendislere matematiksel modellemede kolayliklar saglar. Hemen baslayalim.
Jean Baptiste Joseph, Baron de Fourier, 1768 - 1830
Kendisine Baran de Fourier ismi Napolyon tarafindan verilmis efendim. Bugunku ismiyle bilinen Fourier serisi acilimini madde uzurindeki isi akisi uzerine calisirken buluyor.
Peki Fourier analizine neden ihtiyac duyuyoruz oncelikle bunu irdeleyelim. Simdi efendim, daha onceki yazilardada belirttigimiz gibi bir haberlesme sisteminde ortama salinan bir bilgi mevcut. Bu bilgiyi sinyal olarak isimlendirir isek, ortamimizda hava,su,kablo neyin olabilir. Bu sinyali ortama salma nedenimiz bir alicaya ulasmasini istememizden oturudur. Bir vericiden bir aliciya gonderilen sinyal, kanaldan ve sistemdeki elektronik komponentlerin kararsizliklarindan dolayi distorsiyona yani bozunuma ugrar. Ornegin bir 5volt luk sinyal alicida 3volt seklinde gorulebilir. Yani sinyal uzerine bir gurultu biner. Buraya kadar sinyali hep zaman domeninde varsaydik. Soyle dusunun, yatay eksen zamani, dusey eksen ise sinyalin genlik degerini gostersin (ornegin volt ya da amper cinsinden olabilir.) Simdi bu sinyali frekans domeninde analiz etmek, zaman domeninde analiz etmekten daha kolaydir. Bir soru duyar gibiyim: analiz etmek derken ne demek istiyorsun kardesim?
Bir sinyali analiz etmek o sinyalin tasidigi bilgiyi bulmak, istatistiksek ozelliklerini bulmak, tasidigi enerjiyi bulmak gibi anlamlara gelebilir. Fourier donusumude zaman domenindeki sinyali frekans domeninde gormemizi sagladigi icin, uzerinde onemle durulmasi gereken bir konudur efendim.
Daha da ilerlemeden once isimiz hep sinus ve cosinus lerle olacagi icin, bu iki trigonometrik fonksiyon hakkinda bilmedikleriniz varsa, tamamlamanizi tavsiye ederim. Biz kabaca hatirlayalim.
A*sin(2*pi*f*t + n)
Efendim yukarida yazdigimiz sinusun 3 onemli parametresi vardir. Bunlar genligi, frekansi ve fazidir.
A=genlik
f=frekans
n=faz
Ayni ozellikler cosinus fonksiyonu icinde gecerlidir. Arkadaslar A dedigimiz genlik, bir sunisoidalin maximum genligidir. Frekansi olan f ise, bu sinusun birim zamanda kendi kendini kac defa tekrar ettigini gosterir. Ornegin frekansi yuksek olan bir sinus dusuk olana gore birim zamanda daha cok tekrar yapar. Faz ise zamanla ilgili bir kavramdir. Bir sinusu zamanda bir miktar geciktirirseniz fazini degistirmis olursunuz. Ornegin 0 fazla gonderdiniz bir sinusoidal, kablosuz haberlesme kanalinda gecikmeli olarak alinirsa (alici tarafindan) fazi artik degismis olacaktir.
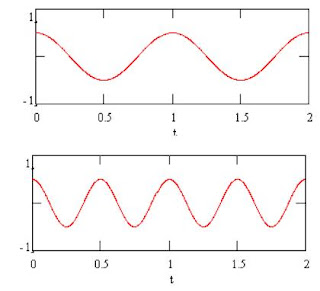
Yukarida uc tane sinusoidal goruyorsunuz. Bunlar hakkinda kisaca yorum yapalim. Soldan saga 1,2,3 diye numaralandirirsak eger, genligi en yuksek olan 1, en dusuk olan ise 2 dir. Frekansi en yuksek olan (dikkat edin her uc sinyalde zaman ekseninde 0 ile 4sn arasinda) 2 ve en dusuk olan 1 numaradir. Hepsinin fazi ise 0 dir. Simdi yavas yavas fourieri detaylandirmaya baslayalim.Arkadaslar kendimizi receiver(alici) yerine koyalim. Cok komplike bir sinyal geciyor elimize. Gorevimiz bu sinyalin icindeki bilgileri alip kullaniciya iletmek. Iste Fourier sunu farkediyor, biz bu kompleks sinyalleri sinusoidallerin toplami olarak yazabiliriz, dolayisiyla elimizde uzerinde islem yapabilecegimiz matematiksel bir model bulunur. Ornegin su sinyale bir goz atin;
Yukarida gordugunuz sinyal zaman domeninde 0 ve 4. saniyeler arasinda ve periyodik bir sinyaldir yani bir zaman araligindan sonra kendini tekrar ediyor. Bu sinyal aslinda 3 tane, genlikleri,frekanslari ve fazlari farkli sinusoidal sinyalin toplami olarak ifade edilebilir. Bu 3 sin ise ilk seklimizde verdigimiz sin lerdir. Sabirsizlandiginizi farkediyorum. Diyorsunuz ki ama hani nerde frekans domenine donusum. O zaman asagidaki sekli bir inceleyelim.
Evet sari okun gosterdigi yonden bakarsaniz eger bu 3 sinusun toplamindan olusan sinyali frekans domeninde, turkuaz renkli okun yonunden bakarsaniz zaman domeninde gorursunuz. Frekans domenine bakinca sanki genlikleri (dikey eksen) ve frekanslari (yatay eksen) farkli (gercektende 3 sinisunde genlikleri ve frekanslari farkli) 3 tane cubuk goruyor gibi olacagiz. Yani soyle olacak;
(Bu arada bir sinyalin frekans domenindeki gosterimine o sinyalin spektrumu da deniyor, aklinizda buluna.)
O zaman gelin bir tanim yapalim. Herhangi bir PERIYODIK sinyal, bircok farkli veya ayni genlik,faz,frekanstaki sinusoidal (sin,cos) sinyallerin toplami olarak gosterilebilir. Bu toplama Fourier serisi diyelim. Yukaridaki sekilde gordugunuz yatay eksende yazan her uc sinisun genlik(amplitude) degerleri iste fourier serisi formulundeki fourier katsayilarina tekabul ediyor :). Sekildede goruldugu gibi sinyalin spektrumu sadece pozitif frekanslari barindiriyor. Simdi diyeceksiniz ki negatif frekansta mi var? Efendim hersey bizlere kolaylik olsun diye. Bu konuya ileride deginecegiz. Simdi gelin birde bir baska cok komplike bir sinyali (zaman domeninde) inceleyelim. Sinyalimiz su;
Sekle dikkatli bakarsaniz eger, yatay eksen (saniye cinsinden olsun) zaman, dusey eksen ise her bir zaman dilimine tekabul eden genlik degerleridir ve sinyalimizin periyodu 1 saniyedir yani her 1 saniyede bir kendini tekrar etmektedir. Yani sinyalimiz PERIYODIK bir sinyaldir arkadaslar. O zaman biz bu sinyalide sinisoidal sinyallerin toplami olarak gosterebiliriz.
Simdi 4 tane sinus goeceksiniz asagida, bir inceleyin bakalim.
Frekansi 1 Hz, Genligi 1 Volt
Bu 4 sinisun herbirinin frekansi bir tamsayi. Daha bilimsel konusursak eger her sinis birbirinin HARMONIK i (muzik notalarinda kullanilan harmoniklere benzer sekilde.) Peki HARMONIK ne demek bir bakalim.
Harmonik nedir? : Harmonik diger frekanslarin tam kati olan bir frekanstir. Ornegin 2 ve 4 Hz, 1 Hz in harmonigidir, cunku 1 Hz in tamsayi katidir. Ayni sekilde 3.6 ve 2.4 Hz de 1.2 Hz in harmonigidir cunku her ikiside 1.2 nin tamsayi katlaridir. Burda birde tek harmonik ve cift harmonik kavramina deginelim. 2.4 Hz, 1.2 Hz in cift sayi (2) kati oldugu icin cift harmonigidir ancak 3.4 Hz, tek sayi (3) kati oldugu icin tek harmonigidir. 66,110 ve 154 Hz frekanslari 22 Hz in tek harmonikleri iken, 44,88, 132 Hz cift harmonikleridir. Gordunuz gibi basit bir kavram. Simdi bu harmoiklerin toplamini nasil gosteriyoruz ona bakalim. Bu harmoniklerin toplamlari olan sinyalimizi (daha once bir sinyali sin lerin toplami seklinde gosterdigimizi, bununda fourier serisi acilimi oldugundan bahsetmistik) su sekilde gosteriyoruz;
F(t) yi olusturan sinuslerden her birisi baslangic frekansi olan W(omega, dabilyu degil) nin tamsayi katidir. Bu arada W ya acisal frekans diyoruz ve W=2*pi*f seklinde gosteriyoruz(o zaman f=1 Hz olan sinus baslangic frekansidir ve 2,3,4 hz frekanslarida 1 hz lik sinusun harmonikleridir). f(t) yi yukarida ardarada verdigimiz 4 sinusun toplami olarak dusundugumuzde, yukaridaki formulu su sekilde acabiliriz;
f(t)=sin(2*pi*1*t)+sin(2*pi*2*t)+sin(2*pi*3*t)+sin(2*pi*4*t)
Dikkat ederseniz hepsinin genligi 1, hepsinin baslangic fazi 0 derecedir. Bu 4 sinusu yukarida altalata vermistik. Simdi bu 4 sinusun toplami nasil bir sinyal oluyor ona bakalim.
Yukaridaki grafik 4 sinusun toplami olan zaman domenindeki sinyaldir. Simdi suna dikkat edin. Bu sinyalin frekans domeninde ki gorunumu 1,2,3 ve 4 hz te 4 tane cubuktan olusacakti. Boylece Fourier sayesinde zaman domenindeki sinyalin, frekans domeninde, hangi frekanslarda kac tane sinusoidden meydana geldigini gorebiliyoruz. Fourierin mantigi budur arkadaslar, gordugunuz gibi cok his ve zekice. Devam edelim. Simdi 4 degilde 25 tane ayni genlikteki sinusu birbirine ekleyelim. Elde edecegimiz sinyal budur;
Evet, 25 sinusun toplami bu sekilde oluyor. Dikkat ederseniz, genligi 1 olan 4 sinyali topladigimizda elde ettigimiz sinyalin max genligi 4, 25 sinyali topladigimizda (genligi 1 olan) max genligimiz 25 oldu. Bir diger dikkat etmemiz gereken durum, fourieri hep periyodik sinyaller icin kullandik. Son iki sekle bakarsaniz, periyodikligi goreceksiniz. Simdi farkli bir sey deneyelim. Topladigimiz sinuslerin genliklerini hep esit ve 1 olarak kabul ettik. Ancak bu durum pek gercekci degil onun icin biz farkli genlikler ve frekanslardaki sinusleri ele alalim. O zaman f(t) yi tekrar formuluze edersek;
elde edecegiz. Artik her sinus icin farkli bir genlik degerimiz var ve bunu 'a' ile gosterdik. Daha once esit genlikli 4 sinusu toplayarak elde ettigimiz sinyal, farkli genliklerde ki 4 sinusu toplayinca su sekle gelecek;
Simdi gene cok onemli bir konuya deginecegiz. Yukarida da gordugunuz gibi, kac tane sinusu eklerseniz ekleyin, sinyal hep sifir degerinden baslar. Ancak bizim boyle bir zorunlulugumuz olmamali. Yani sinyalimiz t=0 da nonzero dedigimiz, sifirdan farkli bir sayidan da baslayabilmeli. Bunu yapabilmek icinde cos leri devreye sokacagiz. Bildiginiz gibi sifir fazli cosinus t=0 da sifirdan farkli bir degerden basliyor. O zaman cosinusleri de toplama eklersek sinyalin t=0 daki degerini nonzero yapabiliriz. Simdi daha once genligi 1 ve frekanslari sirasiyla 1,2,3,4 olan sinusleri topladimiz gibi genligi 1 ve frekanslari sirasiyla 1,2,3,4 olan cosinusleri toplayalim. Once bunlari gorelim;
Bu 4 cosinusun toplamini asagida ve, gene genlikleri 1 frekanlari farkli 30 cosinusun toplaminida onun altinda gorebilirsiniz;
Peki cosinuslerin genlikleri esit mi olacak her zaman? Tabii ki Hayir. Cunku sinusler icinde soylemistik, genliklerin esit olmasi hic gercekci bir durum degil. O zaman f(t) nin formulunu tekrar yazalim. Ne degisiklik yaptik? Sinuslere ek olarak cosinusleri de topladik ve genliklerini de farkli aldik. O zaman f(t) soyle olacak:
Artik kafanizda Fourier serisi yavas yavas sekilleniyordur. Simdilik bu kadar. Buradan devam edecek!












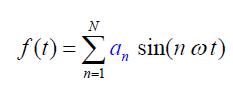





Hiç yorum yok:
Yorum Gönder